Geometria das transformações

Nas últimas seis edições, as reportagens da série Temas Desafiadores explicaram como ensinar conteúdos de Matemática que fazem parte do currículo dos anos finais do Ensino Fundamental e são considerados complexos pelos estudantes e por muitos professores.

Com a afirmação "as propriedades das figuras planas e o cálculo de área e de perímetro são insuficientes para sustentar o estudo da geometria", Humberto Luis de Jesus, assessor técnico da Secretaria Municipal de Educação de São Paulo, ajudou NOVA ESCOLA a eleger o tema da última reportagem da série: geometria das transformações e os conceitos de reflexão, translação e rotação (congruência) e homotetia (semelhança).

Trata-se de um assunto que colabora com o desenvolvimento da percepção espacial da turma, assim como com a capacidade de elaboração de uma linguagem própria da área e a aprendizagem das formas de fazer a representação gráfica de imagens. E mais: ter uma base consistente a esse respeito ajuda a dominar outros saberes explorados mais adiante no Ensino Médio, como coordenadas no plano cartesiano e funções.

As maiores dificuldades encontradas pela turma na compreensão desses conteúdos são em relação a como lidar com os conceitos na resolução de problemas indo além das simples definições.

É claro que elas são importantes e colaboram com o entendimento do tema, mas o ideal é saber como usá-las como uma ferramenta para resolver as questões, em vez de somente aplicá-las como respostas prontas (leia na última página dois problemas e alguns possíveis equívocos cometidos pelos estudantes).

• Leia também: Copa do Mundo e Matemática: veja como aliar futebol às atividades de Geometria

Humberto lembra também que o tema é rico para fazer conexões entre a Matemática, as artes e a engenharia e que o seu aprendizado pode ocorrer por meio de inúmeras aplicações. Para trabalhar o tema em sala, porém, não basta fazer conexões com contextos cotidianos ou pedir que a turma encontre as transformações geométricas nos objetos. O conhecimento não é intuitivo.

Geometria: congurência e semelhança têm a ver com posição e tamanho

Duas imagens congruentes são aquelas que, quando sobrepostas, é possível verificar a correspondência entre as medidas de lados e ângulos e a manutenção da forma e do tamanho. A diferença se dá apenas em relação à posição. Imagens congruentes fazem parte de uma rede chamada transformações isométricas (ou simetrias), que por sua vez é dividida em três naturezas:

Reflexão (ou simetria axial)

De uma maneira simplificada, trata-se do espelhamento de uma figura. Mas não basta a turma saber isso. É preciso compreender que o eixo de simetria pode determinar como se dá a reflexão, divide um plano em dois e separa uma imagem original de seu reflexo, conservando a forma, o ângulo e o tamanho - deixando uma invertida em relação à outra.

As figuras refletidas têm um ponto correspondente a outro em cada lado do eixo e mantêm a mesma distância em relação ao eixo de simetria. Observe o exemplo a seguir:

Para construir uma imagem refletida tendo uma figura e seu eixo, é possível dobrar a folha em que ela está desenhada sobre o eixo de simetria do desenho e copiá-la no lado oposto.

Outra maneira que mobiliza outros saberes geométricos é traçar uma reta perpendicular ao eixo, passando pelos pontos da imagem original, e marcar, no lado oposto, sua posição, mantendo a mesma distância do segmento. É preciso eleger pontos que servirão de referência para o desenho da figura transformada (leia a sequência didática).

Rotação

Nessa transformação, parece que a imagem está desenhada em outra posição, fazendo um giro em relação à original. Mas a ideia está incompleta. Não contempla o que determina o posicionamento da figura, o centro da rotação. Veja a imagem abaixo:

Para obedecer a proposta de rotacionar uma figura a 90° no sentido horário, o centro deve ser o ponto de partida para medir o ângulo determinado - e assim a imagem inteira é transportada para outro local, ocupando uma posição diferente.

Dessa forma, são encontrados os pontos correspondentes aos originais e mantidas as mesmas medidas entre o centro e a nova figura. Essa transformação mostra como resultado imagens congruentes, com os ângulos e os lados correspondentes medindo o mesmo valor e partindo de um mesmo centro.

• Leia também: Matemática: a Geometria da Arte

Translação

À primeira vista, parece só se tratar da mesma figura copiada ao lado da original. Porém existem alguns detalhes que fazem essa transformação ser mais que isso. Observe a imagem:

Trata-se de repetição, porém a mesma figura tem de ser repetida uma ou mais vezes em intervalos regulares, como se estivesse deslizando a certa distância, em uma mesma direção.

Para aplicar o conceito, é necessário saber as medidas dos segmentos e dos ângulos do original e traçá-los de forma idêntica, conservando a forma e o tamanho. A nova imagem terá como diferença a posição, podendo estar mais à esquerda ou à direita, para baixo ou para cima ou inclinada da original.

Se nos casos anteriores, as imagens se mantinham congruentes, quando o assunto é semelhança, embora a forma, o ângulo e a posição sejam preservados, o tamanho é alterado.

Essas possibilidades são as homotetias, subdivididas em ampliação e redução. Em ambos os casos, o que marca a mudança é a proporcionalidade, ou seja, se um quadrado com 1,5 centímetro de lado tiver seu comprimento de lado dobrado (razão 1:2), os lados da nova imagem têm de ter 3 centímetros de lado. Observe o exemplo abaixo:

Discutir diferentes situações e sistematizar os conceitos

Numa atividade em que os alunos devem fazer duas reflexões em retas paralelas, uma possibilidade para enriquecer o exercício é solicitar que analisem o que a figura final representa (uma translação do primeiro desenho). Assim, você possibilita a relação de congruência com reflexão e translação.

"A composição de várias transformações pode criar padrões geométricos interessantes de serem analisados e construídos", diz Marcio Antonio da Silva, docente da Universidade Federal de Mato Grosso do Sul (UFMS).

Os problemas também devem incluir a construção de outras figuras e ainda a manipulação de objetos. Outra proposta é usar os trabalhos do artista holandês Maurits Escher (no quadro abaixo, saiba como analisar as obras de Escher com a turma).

É essencial ainda saber que é preciso manter o original como um padrão rígido. "Régua, transferidor, esquadro e compasso devem ser usados tanto pelo professor, no quadro, como pela turma", diz Andréia Brito, professora da EEEFM Carlos Drumond de Andrade, em Presidente Médici, a 412 quilômetros de Porto Velho.

O contato com a variedade de propostas vai colaborar para que, no momento da sistematização dos conceitos, os jovens tenham uma bagagem ampla e saibam enfrentar os obstáculos que surgirem. É assim que eles vão assimilar conteúdos, abstrair imagens e refletir a respeito das características conceituais.

O trabalho com transformações geométricas de Escher

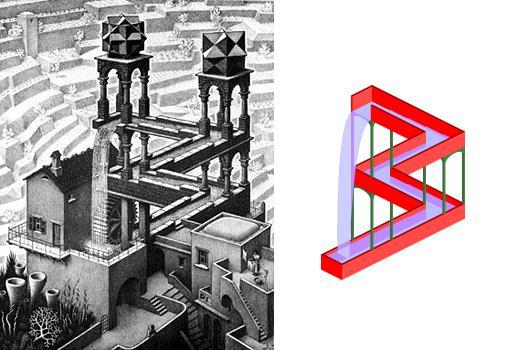
O artista holandês Maurits Escher (1898-1972) construía gravuras utilizando conceitos da geometria da transformação. As imagens abaixo mostram uma de suas obras e um esquema feito por Andrew Kepert, professor de Matemática da Universidade de Newcastle, na Austrália, que simplifica a relação entre os quadros queda d'água desenhada.

Na figura à esquerda, a técnica de pintura deixa evidente o efeito de tridimensionalidade, passando a ideia de que a água sobe pelas canaletas, faz curvas e cai como uma cachoeira. Na imagem à direita, é mais fácil analisar o que Escher fez para conseguir passar a ideia movimento: as imagens se repetem e cada segmento sofre uma rotação a 90°.

Com a obra acima, os alunos podem debater por quais transformações uma mesma figura plana passa e quais efeitos surgem de suas movimentações. "Nas obras do Escher, vale observar com a turma quais são os padrões de imagens e de quais formas elas se apresentam", explica Silva. No site oficial de M.C.Escher  (em inglês), dentro da galeria de imagens ( Picture Gallery), pode-se encontrar gravuras do artista para explorar os padrões de figuras e como elas se transformam. 
 

 

Enunciados, respostas equivocadas e análises

Nos problemas abaixo, foram explorados os conceitos de reflexão e translação. Veja alguns equívocos que os alunos podem cometer e por quê.

Um pintor precisa registrar a palavra AMBULÂNCIA na frente de um veículo. De que maneira ele deve escrever para que, no trânsito, o motorista do carro da frente consiga ler o texto corretamente pelo retrovisor?

Comentário O aluno acertou ao inverter as letras da figura, colocar a nova palavra na mesma distância da original e manter o tamanho da figura. Porém refletiu as letras uma a uma, sem considerar que todas juntas é que formam a imagem que precisa ser compreendida ao ser refletida no retrovisor. O correto é

Observe o desenho abaixo, o piso de uma casa. Responda: existe simetria? Justifique sua resposta.

Não, porque as estampas não estão invertidas.

Comentário
O aluno confundiu reflexão com translação. Ele deveria ter identificado o padrão de repetição. Há imagens se repetindo na diagonal, segundo um segmento orientado da mesma medida, e na direção horizontal, também de acordo com um segmento orientado da mesma medida. Ou seja, existe simetria.