Resolução da retomada
Plano de Aula
Plano de aula: A Geometria do Táxi e a distância entre pontos
Plano 5 de uma sequência de 5 planos. Veja todos os planos sobre Distância entre dois pontos no plano cartesiano
Por: Lara Martins Barbosa
Tem interesse no tema "Neurociência, adolescências e engajamento nos Anos Finais"?
Inscreva-se neste tema para receber novidades pelo site e por email.
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Lara Martins Barbosa
Mentor: Lara Martins Barbosa
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
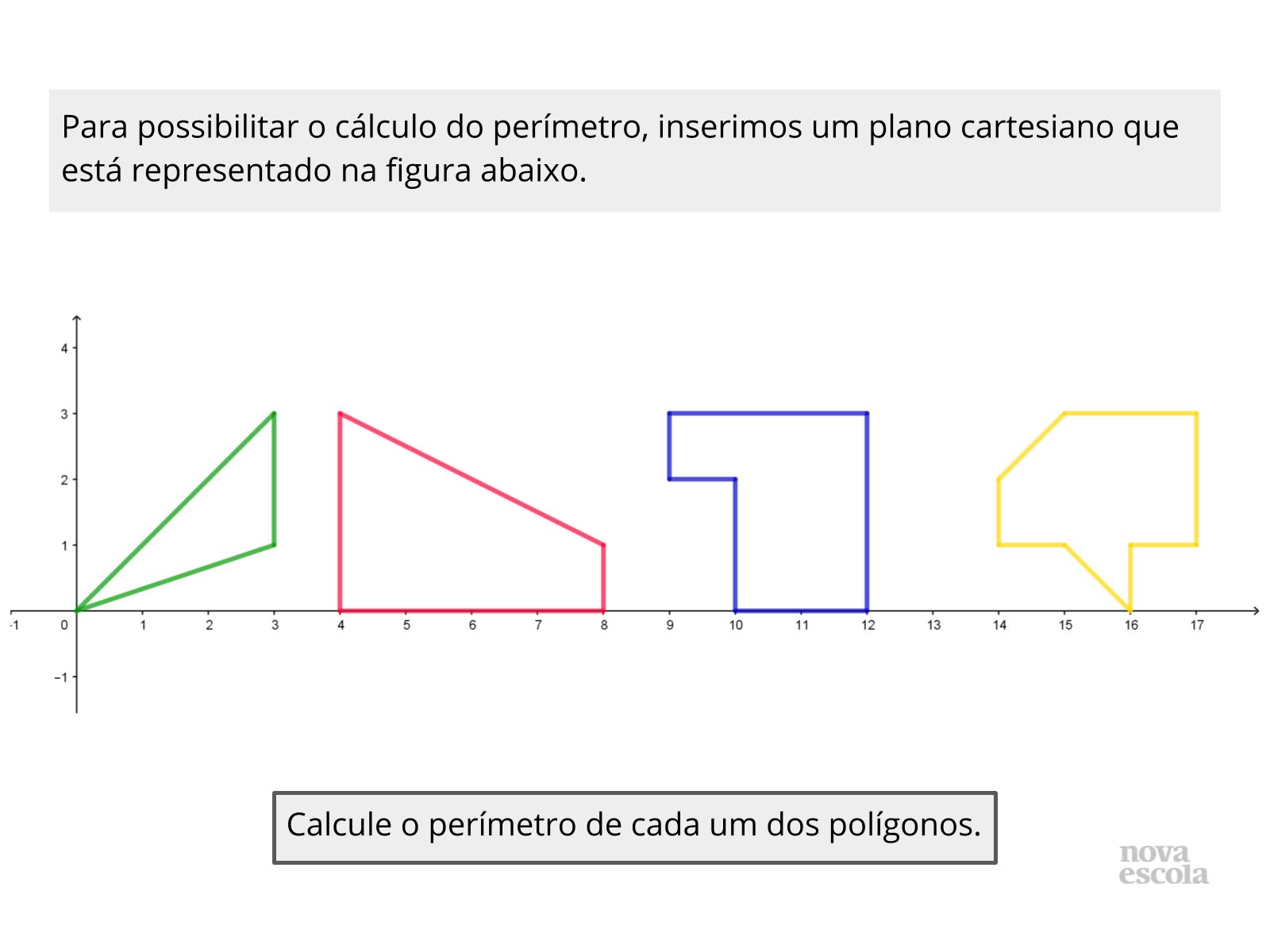
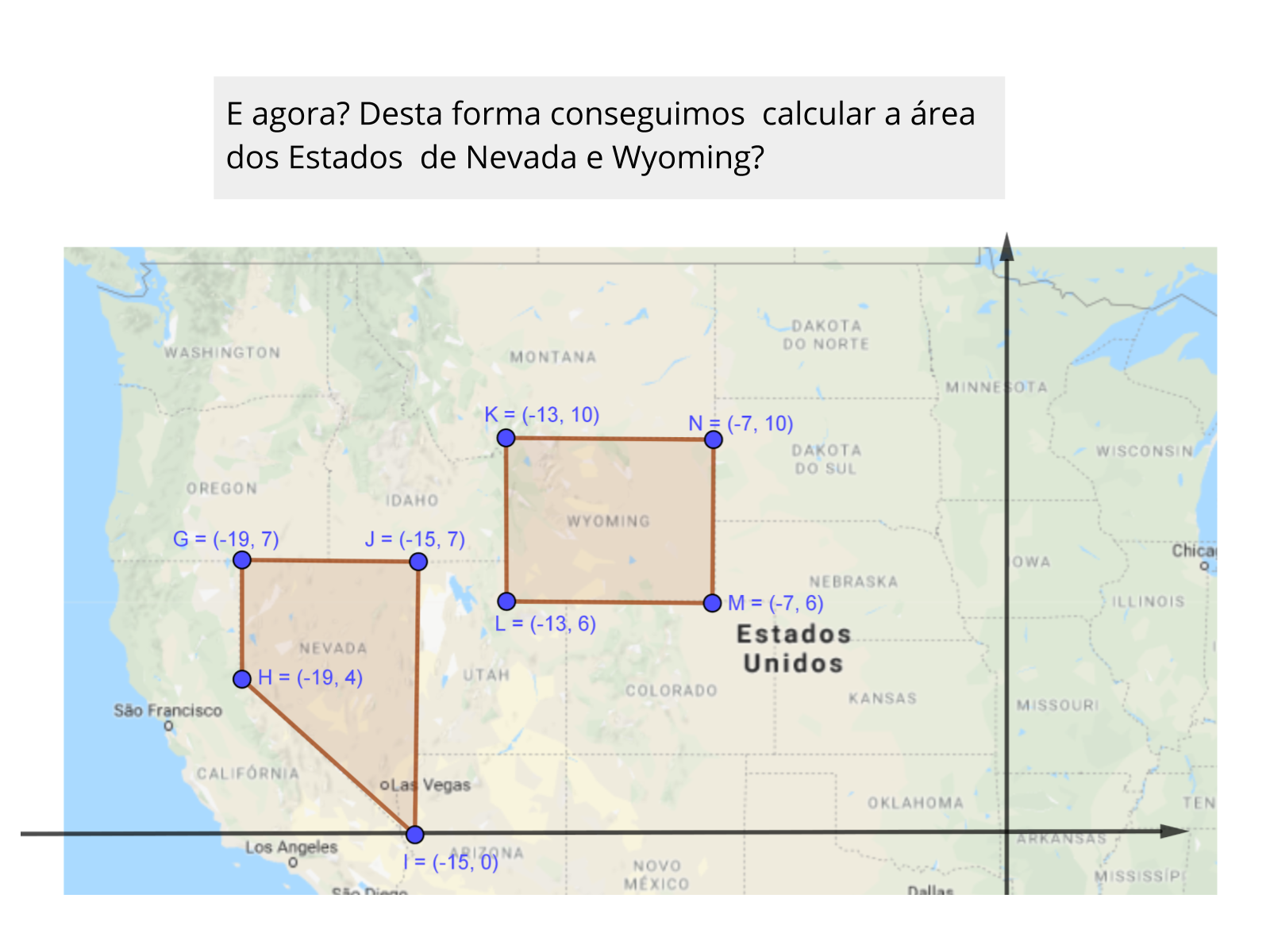
(EF09MA15) - Determinar o ponto médio de um segmento de reta e a distância entre dois pontos quaisquer no plano cartesiano, sem o uso de fórmulas, e utilizar esse conhecimento para calcular, por exemplo, medidas de perímetros e áreas de figuras planas construídas no plano.
Objetivos específicos
Explorar a Geometria do Taxi
Conceito-chave
Plano cartesiano, segmento de reta, Geometria do Taxi, distância entre pontos.
Recursos necessários
Malha quadriculada, lápis e régua.
Habilidades BNCC:
Objetivos de aprendizagem
Explorar a Geometria do Taxi
Aula
Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo
Tempo sugerido: 2 minutos.
Orientações: Projete ou leia o objetivo para a turma. Professor, na Geometria do Taxi a menor distância entre dois pontos de um plano não é a linha reta, como considerada na Geometria Euclidiana. A distância é medida como a viagem de um táxi numa cidade, cujas ruas estendem-se vertical e horizontalmente em uma quadra ou malha urbana, que convenientemente pode ser associada ao plano euclidiano.
Propósito: Apresentar o objetivo para que fique claro o que se deseja atingir com essa aula.
Novo curso gratuito
Conheça nosso mais novo curso sobre adolescências, neurociência e engajamento nos anos finais
VER CURSO
